
Senior Lecturer in Applied and Computational Mathematics
Queensland University of Technology (QUT), Brisbane, Australia
About Me
I am a research and teaching mathematician, currently appointed as a Senior Lecturer in the School of Mathematical Sciences at Queensland University of Technology (QUT) in Brisbane, Australia. In 2022, I was awarded the JH Michell Medal for distinguished research in applied mathematics by the Australian and New Zealand Industrial and Applied Mathematics (ANZIAM) division of the Australian Mathematical Society (AustMS). From 2015-2018, I held an Australian Research Council (ARC) Discovery Early Career Research Award (DECRA), a three-year research fellowship aimed at supporting promising researchers within five years of completing their PhD. From 2013-2014, I was a postdoctoral research fellow at École Centrale Paris (now CentraleSupélec) one of the top engineering schools in France. In 2014, I was briefly a postdoctoral researcher at Imperial College London within the Applied Modelling and Computation Group (Department of Earth Science and Engineering) before commencing an ongoing position as a Lecturer at QUT in 2015.
Research
I engage in fundamental research in the fields of applied and computational mathematics. Primarily, my research focusses on the study of general deterministic (continuum partial differential equation) and stochastic (discrete random walk) models of advection, diffusion and reaction, concepts used widely in science and engineering to describe how physical quantities move, interact and evolve within a physical medium. As a mathematician, my work develops and applies mathematical results, knowledge, methods and code to simulate and improve the understanding of advection-diffusion-reaction phenomena with a distinct focus on heterogeneous media. My body of research work includes contributions to
- analytical solutions
- model parameterisation
- surrogate models
- multiscale methods
- numerical solutions
- model analysis
- model design
As a former high-achieving mathematics student and now a university mathematician who engages in technical research, I enjoy working on mathematical problems hands-on, which has led to a high number of sole author and first author research papers. Finally, while my research is fundamentally driven by mathematical curiosity, it has found application to modelling and simulating physical phenomena from a diverse range of fields including hydrology, physics, pharmacology, biology, wood science, material science and thermodynamics.
Publications
Preprints
Published
- EJ Carr, Random walk models of advection-diffusion in layered media.
(2025) Applied Mathematical Modelling, 141, 115942.
- DJ Oliver, IW Turner and EJ Carr, A two-dimensional dual-grid mapping method to simulate contaminant transport in heterogeneous groundwater systems.
(2025) Computers and Geotechnics, 179, 106999.
- EJ Carr, Total fraction of drug released from diffusion-controlled delivery systems with binding reactions.
(2024) International Journal of Heat and Mass Transfer, 229, 125712.
- EJ Carr and G Pontrelli, Modelling functionalized drug release for a spherical capsule.
(2024) International Journal of Heat and Mass Transfer, 222, 125065.
- DJ Warne, OJ Maclaren, EJ Carr, MJ Simpson and C Drovandi, Generalised likelihood profiles for models with intractable likelihoods.
(2024) Statistics and Computing, 34, 50.
- DJ Oliver, IW Turner and EJ Carr, Dual-grid mapping method for the advection-diffusion-reaction equation in a heterogeneous medium.
(2024) Computers & Mathematics with Applications, 154, 78-90.
- LP Filippini, MJ Simpson and EJ Carr, Simplified models of diffusion in radially-symmetric geometries.
(2023) Physica A: Statistical Mechanics and its Applications, 626, 129067.
- Y-F Lin, J Huang, EJ Carr, T-C Hsieh, H Zhan and H-L Yu, A temporally relaxed theory of physically or chemically non-equilibrium solute transport in heterogeneous porous media.
(2023) Journal of Hydrology, 620(B), 129432.
- EJ Carr and LP Filippini, Analytical formulas for calculating the thermal diffusivity of cylindrical shell and spherical shell samples.
(2023) International Journal of Heat and Mass Transfer, 202, 123693.
- EJ Carr, Exponential and Weibull models for spherical and spherical-shell diffusion-controlled release systems with semi-absorbing boundaries.
(2022) Physica A: Statistical Mechanics and its Applications, 605, 127985.
- HS Murray, C Drovandi, EJ Carr and P Corry, Statistical modelling of goalkicking performance in the Australian Football League.
(2022) Journal of Science and Medicine in Sport, 25(8), pp. 690-695.
- JJ Klowss, AP Browning, RJ Murphy, EJ Carr, MJ Plank, G Gunasingh, NK Haass and MJ Simpson, A stochastic mathematical model of 4D tumour spheroids with real-time fluorescent cell cycle labelling.
(2022) Journal of the Royal Society Interface, 19, 20210903.
- EJ Carr, DJ VandenHeuvel, JM Wilson and MJ Simpson, Mean exit time in irregularly-shaped annular and composite disc domains.
(2022) Journal of Physics A: Mathematical and Theoretical, 55, 105002.
- EJ Carr, DJ Oliver and MJ Simpson, Approximate analytical solution for transient heat and mass transfer across an irregular interface.
(2022) Communications in Nonlinear Science and Numerical Simulation, 108, 106211.
- STP Psaltis, C Kumar, IW Turner, EJ Carr, TW Farrell, L Brancheriau, H Bailleres and DJ Lee, A new approach for predicting board MOE from increment cores.
(2021) Annals of Forest Science, 78, 78.
- NG March, EJ Carr and IW Turner, Numerical investigation into coarse-scale models of diffusion in complex heterogeneous media.
(2021) Transport in Porous Media, 139, pp. 467-489.
- MJ Simpson, AP Browning, C Drovandi, EJ Carr, OJ Maclaren and RE Baker, Profile likelihood analysis for a stochastic model of diffusion in heterogeneous media.
(2021) Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences, 477, 20210214.
- MJ Simpson, DJ VandenHeuvel, JM Wilson, SW McCue and EJ Carr, Mean exit time for diffusion on irregular domains.
(2021) New Journal of Physics, 23, 043030.
- EJ Carr, Generalized semi-analytical solution for coupled multispecies advection-dispersion equations in multilayer porous media.
(2021) Applied Mathematical Modelling, 94, pp. 87-97.
- C Kumar, STP Psaltis, H Bailleres, IW Turner, L Brancheriau, G Hopewell, EJ Carr, TW Farrell and DJ Lee, Accurate estimation of log MOE from non-destructive standing tree measurements.
(2021) Annals of Forest Science, 78, 8.
- NG March, EJ Carr and IW Turner, A fast algorithm for semi-analytically solving the homogenization boundary value problem for block locally-isotropic heterogeneous media.
(2021) Applied Mathematical Modelling, 92, pp. 23-43.
- EJ Carr, New semi-analytical solutions for advection-dispersion equations in multilayer porous media.
(2020) Transport in Porous Media, 135, pp. 39-58.
- G Pontrelli, EJ Carr, A Tiribocchi and S Succi, Modelling drug delivery from multiple emulsions.
(2020) Physical Review E, 102, 023114.
- EJ Carr, JM Ryan and MJ Simpson, Diffusion in heterogeneous discs and spheres: new closed-form expressions for exit times and homogenization formulae.
(2020) The Journal of Chemical Physics, 153, 074115.
- EJ Carr and JJ Klowss, Finite transition times for multispecies diffusion in heterogeneous media coupled via first-order reaction networks.
(2020) Physical Review E, 102, 012107.
- EJ Carr, Advection improves homogenized models of continuum diffusion in one-dimensional heterogeneous media.
(2019) Physical Review E, 100, 062113.
- EJ Carr and CJ Wood, Rear-surface integral method for calculating thermal diffusivity: finite pulse time correction and two-layer samples.
(2019) International Journal of Heat and Mass Transfer, 144, 118609.
- EJ Carr and G Pontrelli, Drug delivery from microcapsules: how can we estimate the release time?
(2019) Mathematical Biosciences, 315, 108216.
- EJ Carr, Rear-surface integral method for calculating thermal diffusivity from laser flash experiments.
(2019) Chemical Engineering Science, 199, pp. 546-551.
- EJ Carr and MJ Simpson, New homogenization approaches for stochastic transport through heterogeneous media.
(2019) The Journal of Chemical Physics, 150, 044104.
- S McInerney, EJ Carr and MJ Simpson, Parameterising continuum models of heat transfer in heterogeneous living skin using experimental data.
(2019) International Journal of Heat and Mass Transfer, 128, pp. 964–975.
- NG March and EJ Carr, Finite volume schemes for multilayer diffusion.
(2019) Journal of Computational and Applied Mathematics, 345, pp. 206-223.
This paper focusses on finite volume schemes for solving multilayer diffusion problems. We develop a finite volume method that addresses a deficiency of recently proposed finite volume/difference methods, which consider only a limited number of interface conditions and do not carry out stability or convergence analysis. Our method also retains second-order accuracy in space while preserving the tridiagonal matrix structure of the classical single-layer discretisation. Stability and convergence analysis of the new finite volume method is presented for each of the three classical time discretisation methods: forward Euler, backward Euler and Crank–Nicolson. We prove that both the backward Euler and Crank–Nicolson schemes are always unconditionally stable. The key contribution of the work is the presentation of a set of sufficient stability conditions for the forward Euler scheme. Here, we find that to ensure stability of the forward Euler scheme it is not sufficient that the time step $\tau$ satisfies the classical constraint of $\tau \leq h_{i}^2/(2D_i)$ in each layer (where $D_i$ is the diffusivity and $h_i$ is the grid spacing in the ith layer) as more restrictive conditions can arise due to the interface conditions. The paper concludes with some numerical examples that demonstrate application of the new finite volume method, with the results presented in excellent agreement with the theoretical analysis. - STP Psaltis, IW Turner, EJ Carr, TW Farrell, G Hopewell and H Bailleres, Three-dimensional virtual reconstruction of timber billets from rotary peeling.
(2018) Computers and Electronics in Agriculture, 152, pp. 269-280.
Accurately determining the timber properties for products prior to cutting the tree is difficult. In this work we discuss a method for reconstructing a timber billet virtually, including internal features, after it has been peeled into a full veneer (ribbon). This reconstruction process is the first stage in developing a mathematical model for the variation in timber properties within a given tree. The reconstruction of internal timber features is typically achieved through the use of computed tomography (CT) scanning. However, this requires the use of equipment that may be cost-prohibitive. Here we discuss an approach that utilises more readily available equipment for timber processors, including a spindleless lathe and digital SLR camera. In comparison to conventional scanning methods, this reconstruction method based on a destructive process has the key advantage of delivering high-resolution colour images. This reconstruction serves two purposes. Firstly, we are able to generate three-dimensional visualisations of the timber billet, to uncover internal structures such as knots, defects, insect or fungi attack, discoloration, resin, etc. Secondly, the reconstruction allows us to map timber properties measured on the veneer to their original location within the billet. This allows us to locally inform the mapping with wood properties and subsequently derive their distribution throughout the billet. From this information it is then possible to extract any part of the billet and obtain the appearance and wood properties of any processed products. To validate our reconstruction process we show that we can obtain reasonable agreement between our predicted billet modulus of elasticity and that measured on the original billet. - EJ Carr and G Pontrelli, Modelling mass diffusion for a multi-layer sphere immersed in a semi-infinite medium: application to drug delivery.
(2018) Mathematical Biosciences, 303, pp. 1-9.
We present a general mechanistic model of mass diffusion for a composite sphere placed in a large ambient medium. The multi-layer problem is described by a system of diffusion equations coupled via interlayer boundary conditions such as those imposing a finite mass resistance at the external surface of the sphere. While the work is applicable to the generic problem of heat or mass transfer in a multi-layer sphere, the analysis and results are presented in the context of drug kinetics for desorbing and absorbing spherical microcapsules. We derive an analytical solution for the concentration in the sphere and in the surrounding medium that avoids any artificial truncation at a finite distance. The closed-form solution in each concentric layer is expressed in terms of a suitably-defined inverse Laplace transform that can be evaluated numerically. Concentration profiles and drug mass curves in the spherical layers and in the external environment are presented and the dependency of the solution on the mass transfer coefficient at the surface of the sphere analyzed. - EJ Carr and NG March, Semi-analytical solution of multilayer diffusion problems with time-varying boundary conditions and general interface conditions.
(2018) Applied Mathematics and Computation, 333, pp. 286-303.
- EJ Carr, Characteristic time scales for diffusion processes through layers and across interfaces.
(2018) Physical Review E, 97, 042115.
This paper presents a simple tool for characterizing the time scale for continuum diffusion processes through layered heterogeneous media. This mathematical problem is motivated by several practical applications such as heat transport in composite materials, flow in layered aquifers, and drug diffusion through the layers of the skin. In such processes, the physical properties of the medium vary across layers and internal boundary conditions apply at the interfaces between adjacent layers. To characterize the time scale, we use the concept of mean action time, which provides the mean time scale at each position in the medium by utilizing the fact that the transition of the transient solution of the underlying partial differential equation model, from initial state to steady state, can be represented as a cumulative distribution function of time. Using this concept, we define the characteristic time scale for a multilayer diffusion process as the maximum value of the mean action time across the layered medium. For given initial conditions and internal and external boundary conditions, this approach leads to simple algebraic expressions for characterizing the time scale that depend on the physical and geometrical properties of the medium, such as the diffusivities and lengths of the layers. Numerical examples demonstrate that these expressions provide useful insight into explaining how the parameters in the model affect the time it takes for a multilayer diffusion process to reach steady state. - EJ Carr and MJ Simpson, Rapid calculation of maximum particle lifetime for diffusion in complex geometries.
(2018) The Journal of Chemical Physics, 148, 094113.
Diffusion of molecules within biological cells and tissues is strongly influenced by crowding. A key quantity to characterize diffusion is the particle lifetime, which is the time taken for a diffusing particle to exit by hitting an absorbing boundary. Calculating the particle lifetime provides valuable information, for example, by allowing us to compare the timescale of diffusion and the timescale of the reaction, thereby helping us to develop appropriate mathematical models. Previous methods to quantify particle lifetimes focus on the mean particle lifetime. Here, we take a different approach and present a simple method for calculating the maximum particle lifetime. This is the time after which only a small specified proportion of particles in an ensemble remain in the system. Our approach produces accurate estimates of the maximum particle lifetime, whereas the mean particle lifetime always underestimates this value compared with data from stochastic simulations. Furthermore, we find that differences between the mean and maximum particle lifetimes become increasingly important when considering diffusion hindered by obstacles. - EJ Carr and MJ Simpson, Accurate and efficient calculation of response times for groundwater flow.
(2018) Journal of Hydrology, 558, pp. 470-481.
We study measures of the amount of time required for transient flow in heterogeneous porous media to effectively reach steady state, also known as the response time. Here, we develop a new approach that extends the concept of mean action time. Previous applications of the theory of mean action time to estimate the response time use the first two central moments of the probability density function associated with the transition from the initial condition, at image, to the steady state condition that arises in the long time limit, as $t\rightarrow\infty$. This previous approach leads to a computationally convenient estimation of the response time, but the accuracy can be poor. Here, we outline a powerful extension using the first $k$ raw moments, showing how to produce an extremely accurate estimate by making use of asymptotic properties of the cumulative distribution function. Results are validated using an existing laboratory-scale data set describing flow in a homogeneous porous medium. In addition, we demonstrate how the results also apply to flow in heterogeneous porous media. Overall, the new method is: (i) extremely accurate; and (ii) computationally inexpensive. In fact, the computational cost of the new method is orders of magnitude less than the computational effort required to study the response time by solving the transient flow equation. Furthermore, the approach provides a rigorous mathematical connection with the heuristic argument that the response time for flow in a homogeneous porous medium is proportional to $L^{2}/D$, where $L$ is a relevant length scale, and $D$ is the aquifer diffusivity. Here, we extend such heuristic arguments by providing a clear mathematical definition of the proportionality constant. - AL Redman, H Bailleres, BP Gilbert, EJ Carr, IW Turner and P Perré, Finite element analysis of stress-related degrade during drying of Corymbia citriodora and Eucalyptus obliqua.
(2018) Wood Science and Technology, 52 (1), pp. 67–89.
With the use of experimental wood properties and input moisture content field data, a predictive 3D stress–strain finite element analysis (FEA) model was developed allowing to predict the development of stress-related end splitting and surface checking degrade during conventional and vacuum wood drying. Simulations were carried out for two Australian hardwood species, messmate (Eucalyptus obliqua) and spotted gum (Corymbia citriodora), as these species contrast, in terms of wood properties, drying rates and stress degrade susceptibility. The simulations were performed using a 1/8 symmetry model where the full board dimensions are 1900 mm long x 30 mm thick x 100 mm wide. Moisture content field data model simulations were utilised in a three-dimensional FEA model by extruding a 2D moisture content field computed in the T–L plane across the radial direction to create a 3D model. Material mechanical properties and shrinkage were calculated in relation to moisture content, over discrete time intervals, using a quasi-static solver. End split failure was investigated at the board end, and surface check failure at the board surface, using a Tsai–Wu failure criterion. Simulations showed that messmate was more susceptible to end splitting than spotted gum and that conventionally dried messmate was more susceptible to surface checking than vacuum-dried messmate. The same results were observed from drying trials. The locations of predicted surface check failure also matched drying trials and are compared. - MJ Simpson, S McInerney, EJ Carr, L Cuttle, Quantifying the efficacy of first aid treatments for burn injuries using mathematical modelling and in vivo porcine experiments.
(2017) Scientific Reports, 7, 10925.
First aid treatment of burns reduces scarring and improves healing. We quantify the efficacy of first aid treatments using a mathematical model to describe data from a series of in vivo porcine experiments. We study burn injuries that are subject to various first aid treatments. The treatments vary in the temperature and duration. Calibrating the mathematical model to the experimental data provides estimates of the thermal diffusivity, the rate at which thermal energy is lost to the blood, and the heat transfer coefficient controlling the loss of thermal energy at the interface of the fat and muscle. A limitation of working with in vivo experiments is the difficulty of measuring variations in temperature across the tissue layers. This limitation motivates us to use a simple, single layer mathematical model. Using the solution of the calibrated mathematical model we visualise the temperature distribution across the thickness of the tissue. With this information we propose a novel measure of the potential for tissue damage. This measure quantifies two important factors: (i) the volume of tissue that rises above the threshold temperature associated with the accumulation of tissue damage; and (ii) the duration of time that the tissue remains above this threshold temperature.
- EJ Carr, Calculating how long it takes for a diffusion process to effectively reach steady state without computing the transient solution.
(2017) Physical Review E, 96, 012116.
Mathematically, it takes an infinite amount of time for the transient solution of a diffusion equation to transition from initial to steady state. Calculating a finite transition time, defined as the time required for the transient solution to transition to within a small prescribed tolerance of the steady-state solution, is much more useful in practice. In this paper, we study estimates of finite transition times that avoid explicit calculation of the transient solution by using the property that the transition to steady state defines a cumulative distribution function when time is treated as a random variable. In total, three approaches are studied: (i) mean action time, (ii) mean plus one standard deviation of action time, and (iii) an approach we derive by approximating the large time asymptotic behavior of the cumulative distribution function. Our approach leads to a simple formula for calculating the finite transition time that depends on the prescribed tolerance $\delta$ and the $(k-1)$th and $k$th moments ($k\geq 1$) of the distribution. Results comparing exact and approximate finite transition times lead to two key findings. First, although the first two approaches are useful at characterizing the time scale of the transition, they do not provide accurate estimates for diffusion processes. Second, the new approach allows one to calculate finite transition times accurate to effectively any number of significant digits using only the moments with the accuracy increasing as the index $k$ is increased.
- AL Redman, H Bailleres, P Perré, EJ Carr and IW Turner, A relevant and robust vacuum drying model applied to hardwoods.
(2017) Wood Science and Technology, 51 (4), pp. 701-719.
A robust mathematical model was developed to simulate the heat and mass transfer process that evolves during vacuum-drying of four commercially important Australian native hardwood species. The hardwood species investigated were spotted gum (Corymbia citriodora), blackbutt (Eucalyptus pilularis), jarrah (Eucalyptus marginata), and messmate (Eucalyptus obliqua). These species provide a good test for the model based on their extreme diversity between wood properties and drying characteristics. The model uses boundary condition data from a series of vacuum-drying trials, which were also used to validate predictions. By using measured diffusion coefficient values to calibrate empirical formula, the accuracy of the model was greatly improved. Results of a sensitivity analysis showed that the model outputs provide excellent agreement with experimental observation despite the large range of species behaviour and variation in wood properties. This study confirms that the drying rate is significantly improved as a direct result of the enhanced convective and diffusive transfer along the board thickness. Contrary to softwood, it appears that longitudinal migration provides only a secondary effect. Not only is the model able to predict the heat and mass transfer behaviour of a range of hardwood species, it is also flexible enough to predict the behaviour for both conventional and vacuum-drying scenarios. The outcomes of this work provide the hardwood industry with a well-calibrated predictive drying tool that can be used to optimise drying schedules. - EJ Carr, IW Turner and P Perré, Macroscale modelling of multilayer diffusion: using volume averaging to correct the boundary conditions.
(2017) Applied Mathematical Modelling, 47, pp. 600-618.
This paper investigates the form of the boundary conditions (BCs) used in macroscale models of PDEs with coefficients that vary over a small length-scale (microscale). Specifically, we focus on the one-dimensional multilayer diffusion problem, a simple prototype problem where an analytical solution is available. For a given microscale BC (e.g., Dirichlet, Neumann, Robin, etc.) we derive a corrected macroscale BC using the method of volume averaging. For example, our analysis confirms that a Robin BC should be applied on the macroscale if a Dirichlet BC is specified on the microscale. The macroscale field computed using the corrected BCs more accurately captures the averaged microscale field and leads to a reconstructed microscale field that is in excellent agreement with the true microscale field. While the analysis and results are presented for one-dimensional multilayer diffusion only, the methodology can be extended to and has implications on a broader class of problems. - EJ Carr, P Perré and IW Turner, The extended distributed microstructure model for gradient-driven transport: a two-scale model for bypassing effective parameters.
(2016) Journal of Computational Physics, 327, pp. 810-829.
Numerous problems involving gradient-driven transport processes—e.g., Fourier's and Darcy's law—in heterogeneous materials concern a physical domain that is much larger than the scale at which the coefficients vary spatially. To overcome the prohibitive computational cost associated with such problems, the well-established Distributed Microstructure Model (DMM) provides a two-scale description of the transport process that produces a computationally cheap approximation to the fine-scale solution. This is achieved via the introduction of sparsely distributed micro-cells that together resolve small patches of the fine-scale structure: a macroscopic equation with an effective coefficient describes the global transport and a microscopic equation governs the local transport within each micro-cell. In this paper, we propose a new formulation, the Extended Distributed Microstructure Model (EDMM), where the macroscopic flux is instead defined as the average of the microscopic fluxes within the micro-cells. This avoids the need for any effective parameters and more accurately accounts for a non-equilibrium field in the micro-cells. Another important contribution of the work is the presentation of a new and improved numerical scheme for performing the two-scale computations using control volume, Krylov subspace and parallel computing techniques. Numerical tests are carried out on two challenging test problems: heat conduction in a composite medium and unsaturated water flow in heterogeneous soils. The results indicate that while DMM is more efficient, EDMM is more accurate and is able to capture additional fine-scale features in the solution. - EJ Carr and IW Turner, A semi-analytical solution for multilayer diffusion in a composite medium consisting of a large number of layers.
(2016) Applied Mathematical Modelling, 40 (15-16), pp. 7034-7050.
- EJ Carr and IW Turner, Two-scale computational modelling of water flow in unsaturated soils containing irregular-shaped inclusions.
(2014) International Journal for Numerical Methods in Engineering, 98 (3), pp. 157-173.
The focus of this paper is two-dimensional computational modelling of water flow in unsaturated soils consisting of weakly conductive disconnected inclusions embedded in a highly conductive connected matrix. When the inclusions are small, a two-scale Richards’ equation-based model has been proposed in the literature taking the form of an equation with effective parameters governing the macroscopic flow coupled with a microscopic equation, defined at each point in the macroscopic domain, governing the flow in the inclusions. This paper is devoted to a number of advances in the numerical implementation of this model. Namely, by treating the micro-scale as a two-dimensional problem, our solution approach based on a control volume finite element method can be applied to irregular inclusion geometries, and, if necessary, modified to account for additional phenomena (e.g. imposing the macroscopic gradient on the micro-scale via a linear approximation of the macroscopic variable along the microscopic boundary). This is achieved with the help of an exponential integrator for advancing the solution in time. This time integration method completely avoids generation of the Jacobian matrix of the system and hence eases the computation when solving the two-scale model in a completely coupled manner. Numerical simulations are presented for a two-dimensional infiltration problem. - EJ Carr, TJ Moroney and IW Turner, Performance assessment of exponential Rosenbrock methods for large systems of ODEs.
(2013) ANZIAM Journal, 54, pp. C102-C118.
This article studies time integration methods for stiff systems of ordinary differential equations of large dimension. For such problems, implicit methods generally outperform explicit methods because the step size is usually less restricted by stability constraints. Recently, however, a family of explicit methods, called exponential integrators, have become popular for large stiff problems due to their favourable stability properties and the rapid convergence of non-preconditioned Krylov subspace methods for computing matrix-vector products involving exponential-like functions of the Jacobian matrix. In this article, we implement the so-called exponential Rosenbrock methods using Krylov subspaces. Numerical experiments on a challenging real-world test problem reveal that these methods are a promising preconditioner-free alternative to well-established approaches based on preconditioned Newton-Krylov implementations of the backward differentiation formulas. - EJ Carr, IW Turner and P Perré, A dual-scale modelling approach for drying hygroscopic porous media.
(2013) Multiscale Modeling and Simulation, 11 (1), pp. 362-384.
A new dual-scale modeling approach is presented for simulating the drying of a wet hygroscopic porous material that couples the porous medium (macroscale) with the underlying pore structure (microscale). The proposed model is applied to the convective drying of wood at low temperatures and is valid in the so-called hygroscopic range, where hygroscopically held liquid water is present in the solid phase and water exits only as vapor in the pores. Coupling between scales is achieved by imposing the macroscopic gradients of moisture content and temperature on the microscopic field using suitably defined periodic boundary conditions, which allows the macroscopic mass and thermal fluxes to be defined as averages of the microscopic fluxes over the unit cell. This novel formulation accounts for the intricate coupling of heat and mass transfer at the microscopic scale but reduces to a classical homogenization approach if a linear relationship is assumed between the microscopic gradient and flux. Simulation results for a sample of spruce wood highlight the potential and flexibility of the new dual-scale approach. In particular, for a given unit cell configuration it is not necessary to propose the form of the macroscopic fluxes prior to the simulations because these are determined as a direct result of the dual-scale formulation. - EJ Carr, IW Turner and P Perré, A variable-stepsize Jacobian-free exponential integrator for simulating transport in heterogeneous porous media: application to wood drying.
(2013) Journal of Computational Physics, 233, pp. 66-82.
A Jacobian-free variable-stepsize method is developed for the numerical integration of the large, stiff systems of differential equations encountered when simulating transport in heterogeneous porous media. Our method utilises the exponential Rosenbrock–Euler method, which is explicit in nature and requires a matrix–vector product involving the exponential of the Jacobian matrix at each step of the integration process. These products can be approximated using Krylov subspace methods, which permit a large integration stepsize to be utilised without having to precondition the iterations. This means that our method is truly “Jacobian-free” – the Jacobian need never be formed or factored during the simulation. We assess the performance of the new algorithm for simulating the drying of softwood. Numerical experiments conducted for both low and high temperature drying demonstrates that the new approach outperforms (in terms of accuracy and efficiency) existing simulation codes that utilise the backward Euler method via a preconditioned Newton–Krylov strategy. - EJ Carr, IW Turner and M Ilić, Krylov subspace approximations for the exponential Euler method: error estimates and the harmonic Ritz approximant.
(2011) ANZIAM Journal, 52, pp. C612-C627.
We study Krylov subspace methods for approximating the matrix-function vector product $\varphi(tA)b$ where $\varphi(z) = [\exp(z)-1]/z$. This product arises in the numerical integration of large stiff systems of differential equations by the Exponential Euler Method, where $A$ is the Jacobian matrix of the system. Recently, this method has found application in the simulation of transport phenomena in porous media within mathematical models of wood drying and groundwater flow. We develop an a posteriori upper bound on the Krylov subspace approximation error and provide a new interpretation of a previously published error estimate. This leads to an alternative Krylov approximation to $\varphi(tA)b$, the so-called Harmonic Ritz approximant, which we find does not exhibit oscillatory behaviour of the residual error. - EJ Carr, IW Turner and P Perré, A new control-volume finite-element scheme for heterogeneous porous media: application to the drying of softwood.
(2011) Chemical Engineering & Technology, 34 (7), pp. 1143-1150.
An improved mesoscopic model is presented for simulating the drying of porous media. The aim of this model is to account for two scales simultaneously: the scale of the whole product and the scale of the heterogeneities of the porous medium. The innovation of this method is the utilization of a new mass-conservative scheme based on the Control-Volume Finite-Element (CV-FE) method that partitions the moisture content field over the individual sub-control volumes surrounding each node within the mesh. Although the new formulation has potential for application across a wide range of transport processes in heterogeneous porous media, the focus here is on applying the model to the drying of small sections of softwood consisting of several growth rings. The results conclude that, when compared to a previously published scheme, only the new mass-conservative formulation correctly captures the true moisture content evolution in the earlywood and latewood components of the growth rings during drying. - EJ Carr, TJ Moroney and IW Turner, Efficient simulation of unsaturated flow using exponential time integration.
(2011) Applied Mathematics and Computation, 30 (14), pp. 6587-6596.
We assess the performance of an exponential integrator for advancing stiff, semidiscrete formulations of the unsaturated Richards equation in time. The scheme is of second order and explicit in nature but requires the action of the matrix function $\varphi(A) = A^{-1}[\exp(A)-I]$ on a suitability defined vector $v$ at each time step. When the matrix $A$ is large and sparse, $\varphi(A)v$ can be approximated by Krylov subspace methods that require only matrix–vector products with $A$. We prove that despite the use of this approximation the scheme remains second order. Furthermore, we provide a practical variable-stepsize implementation of the integrator by deriving an estimate of the local error that requires only a single additional function evaluation. Numerical experiments performed on two-dimensional test problems demonstrate that this implementation outperforms second-order, variable-stepsize implementations of the backward differentiation formulae.
Research Images

Random walk models of layered advection-diffusion
Source: Carr (2025)
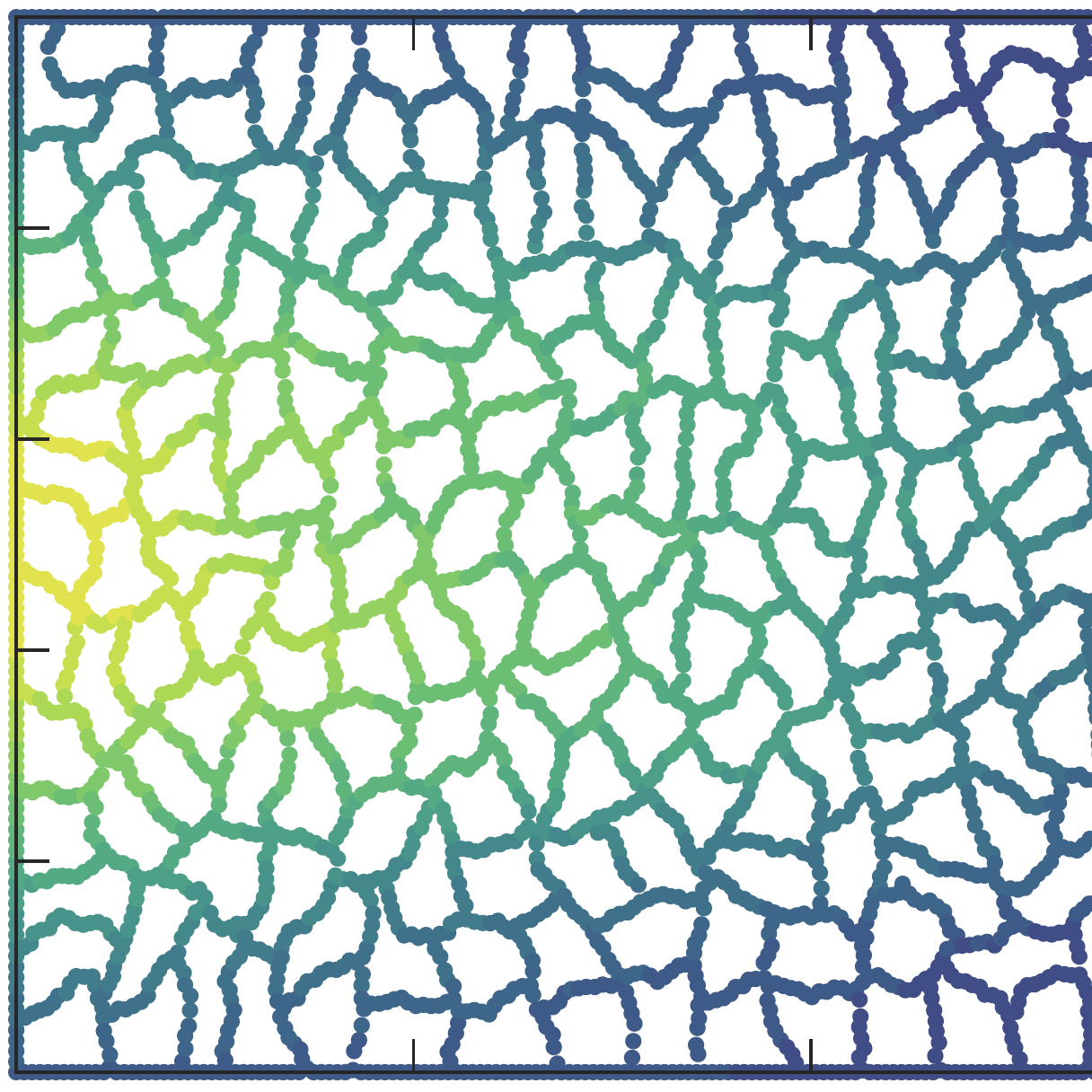
2D dual-grid method for contaminant transport
Source: Oliver et al. (2025)
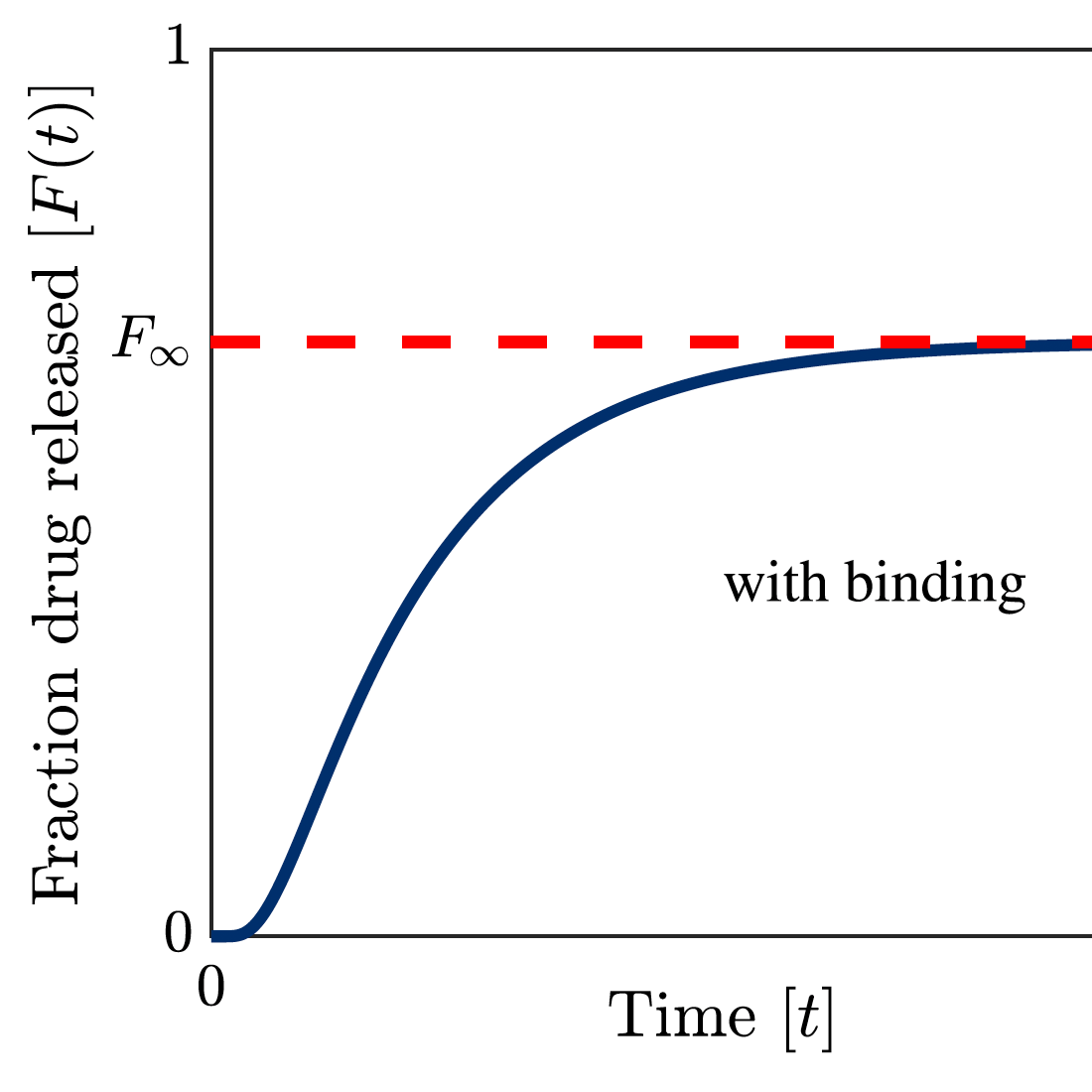
Fraction of drug released under binding reactions
Source: Carr (2024)
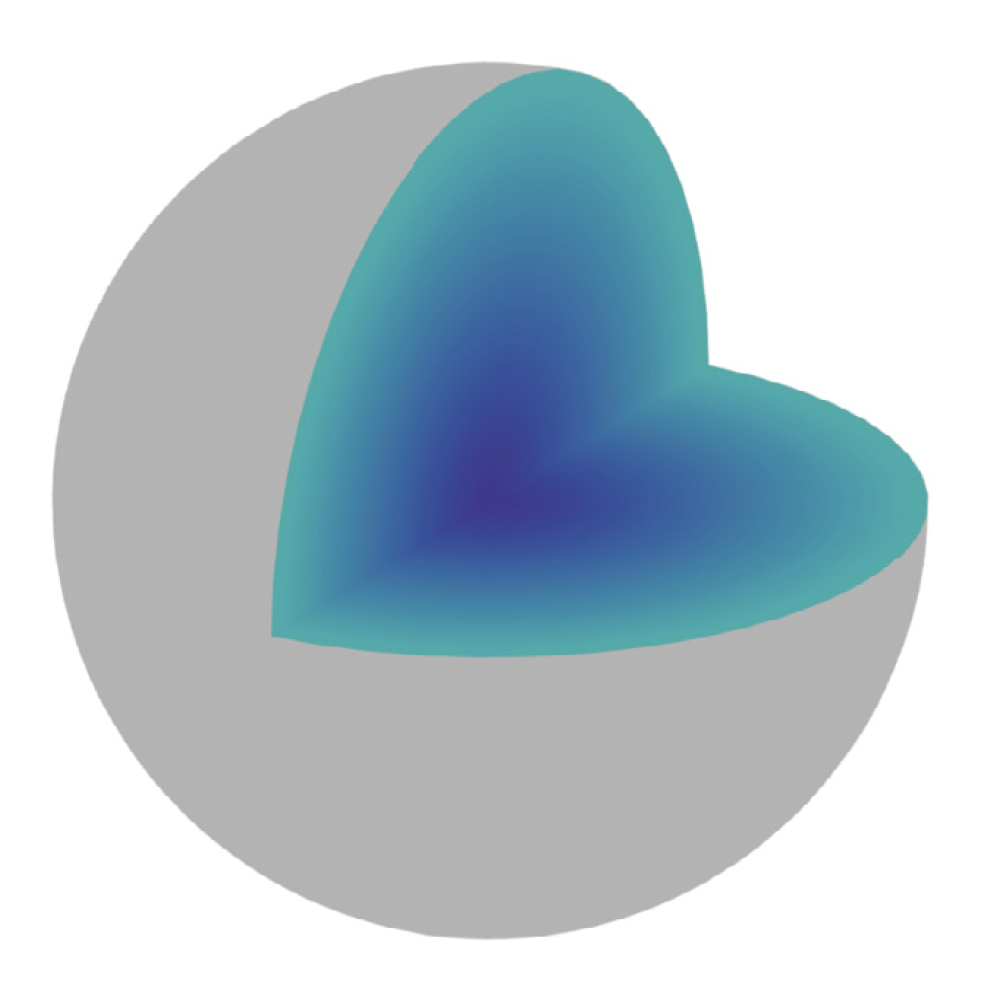
Functionalized drug release for a spherical capsule
Source: Carr and Pontrelli (2024)

1D dual-grid method for advection-diffusion-reaction
Source: Oliver et al. (2024)
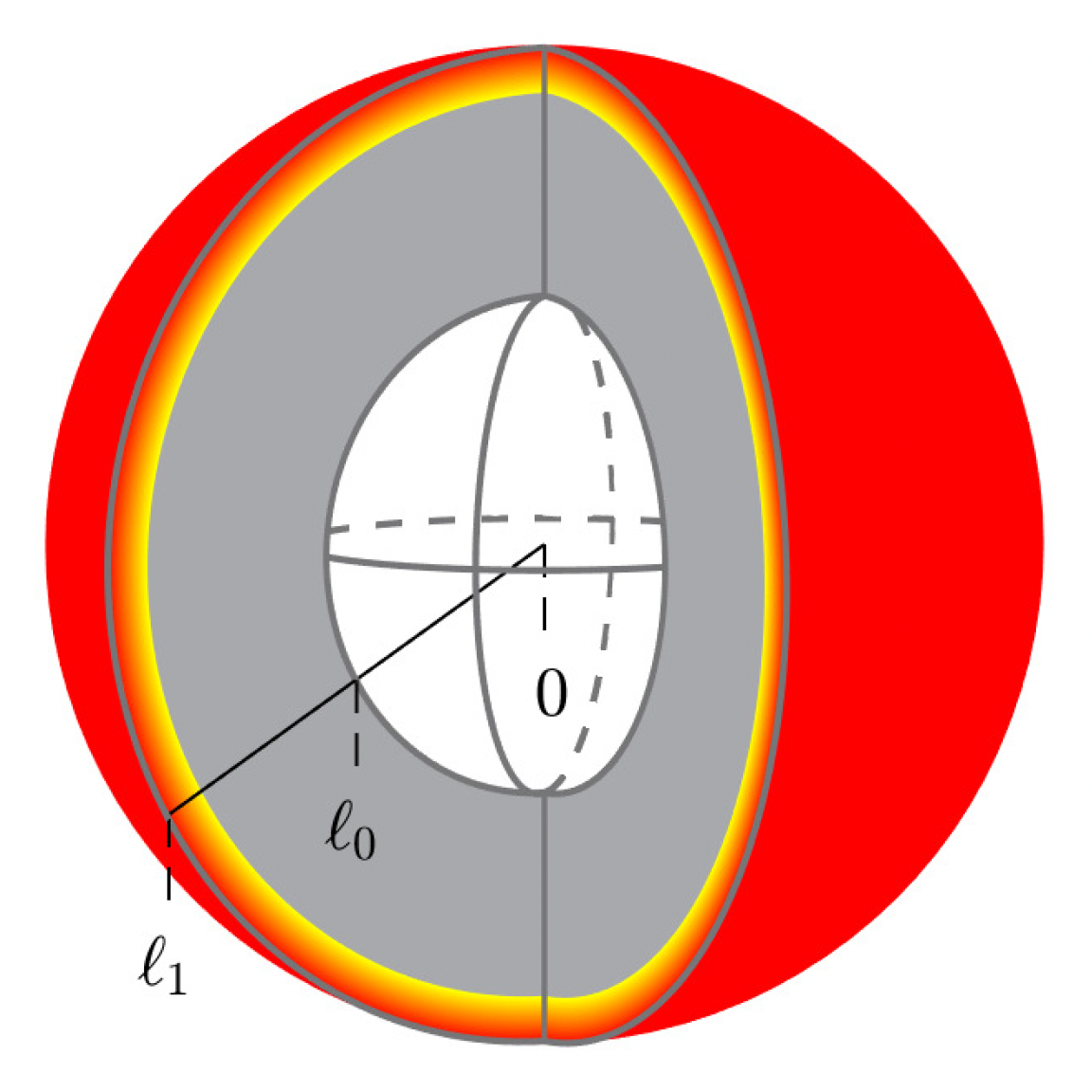
Thermal diffusivity of spherical shell solids
Source: Carr and Filippini (2023)
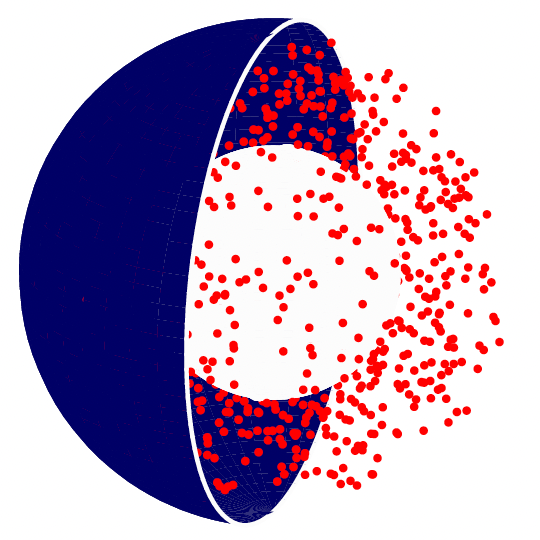
Simplified models of diffusion-controlled release
Source: Carr (2022)
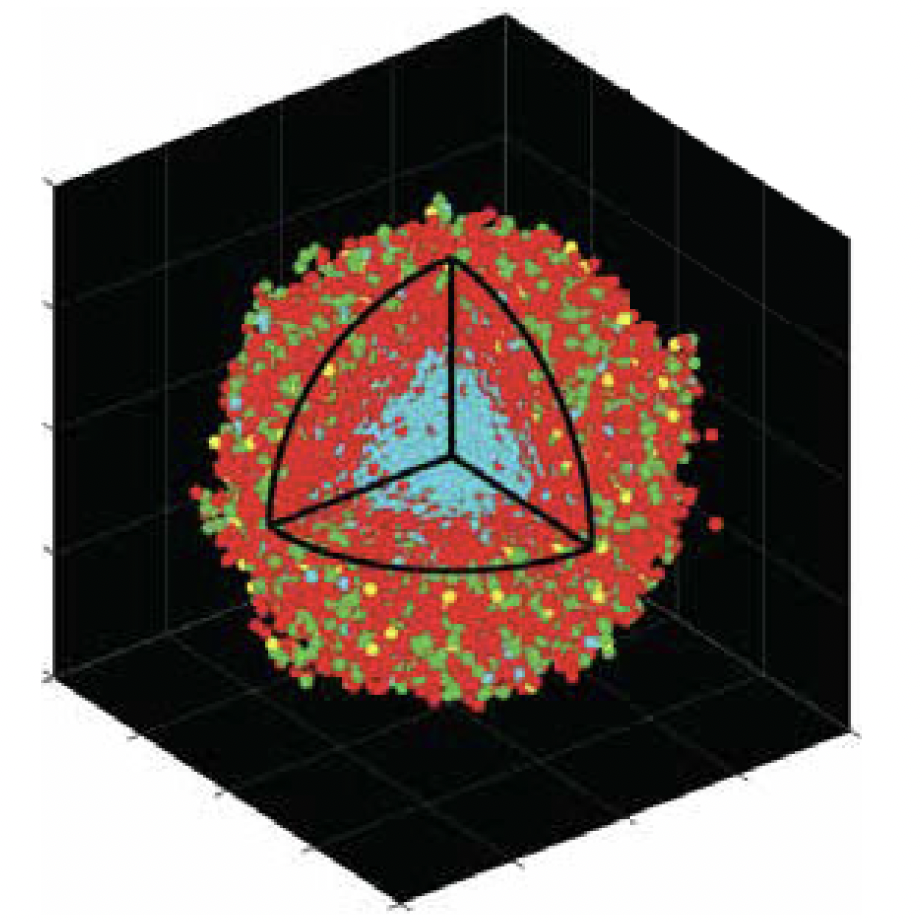
Stochastic model of tumour spheroids
Source: Klowss et al. (2022)
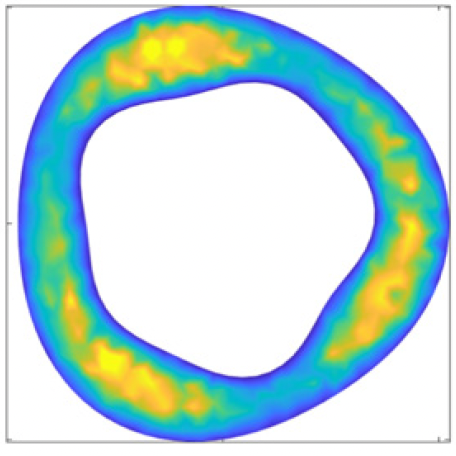
Mean exit time on a perturbed annulus
Source: Carr et al. (2022)
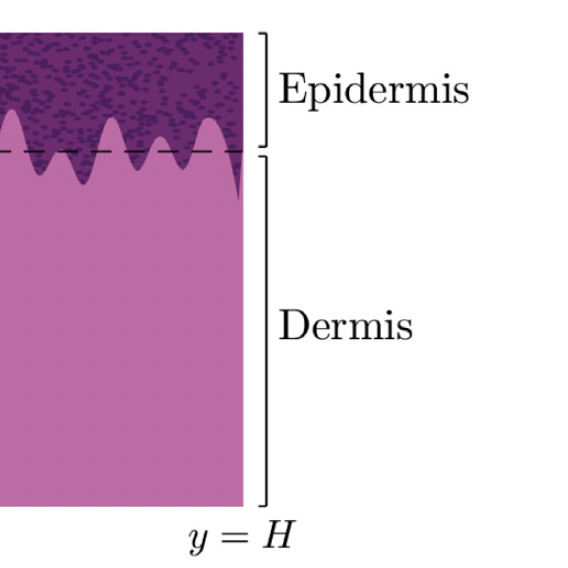
Heat transfer across a perturbed interface
Source: Carr et al. (2022)
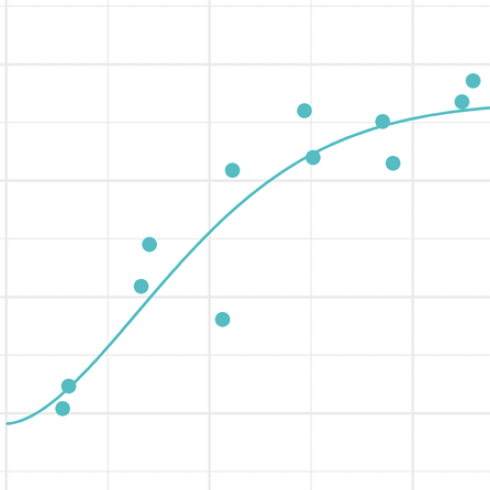
Prediction of wood MOE from core samples
Source: Psaltis et al. (2021)

Diffusion in complex heterogeneous media
Source: March et al. (2021)
Stochastic diffusion in layered media
Source: Simpson et al. (2021)
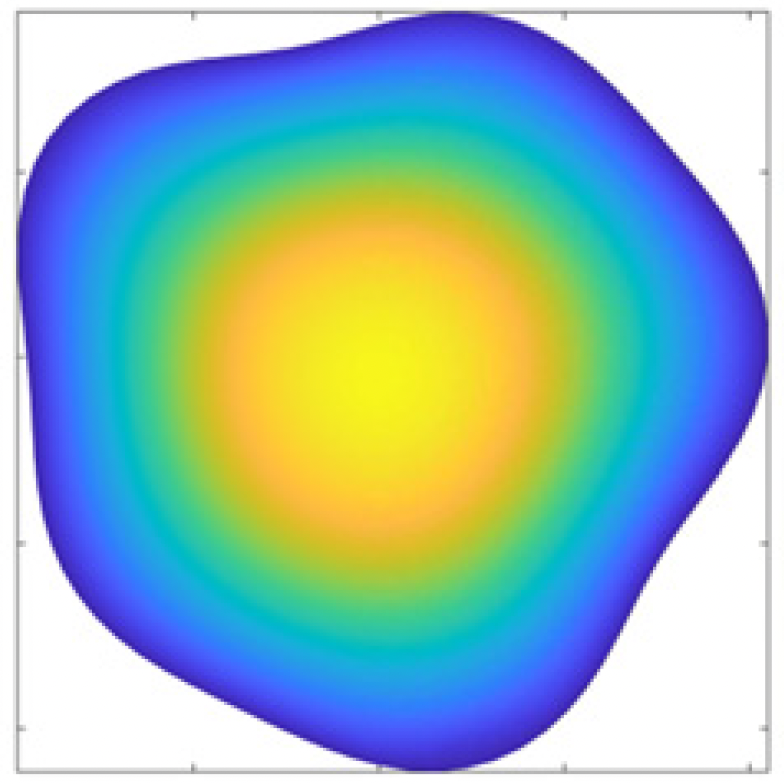
Mean exit time on a perturbed disc
Source: Simpson et al. (2021)
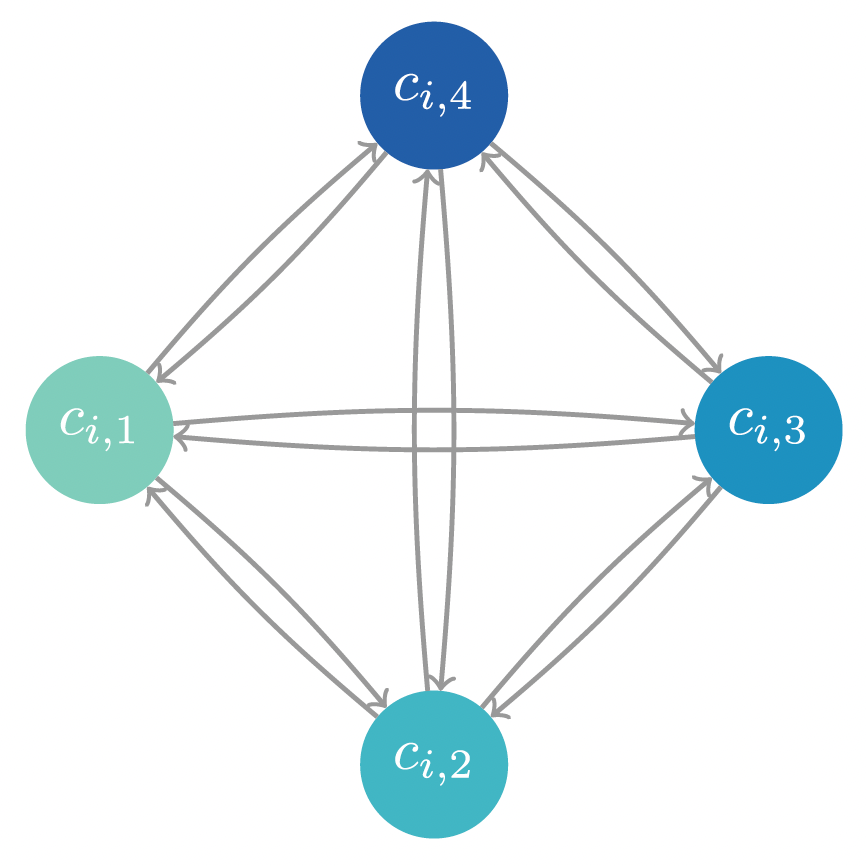
Multispecies advection diffusion reaction
Source: Carr (2021)

Diffusion on block pixellated domains
Source: March et al. (2021)
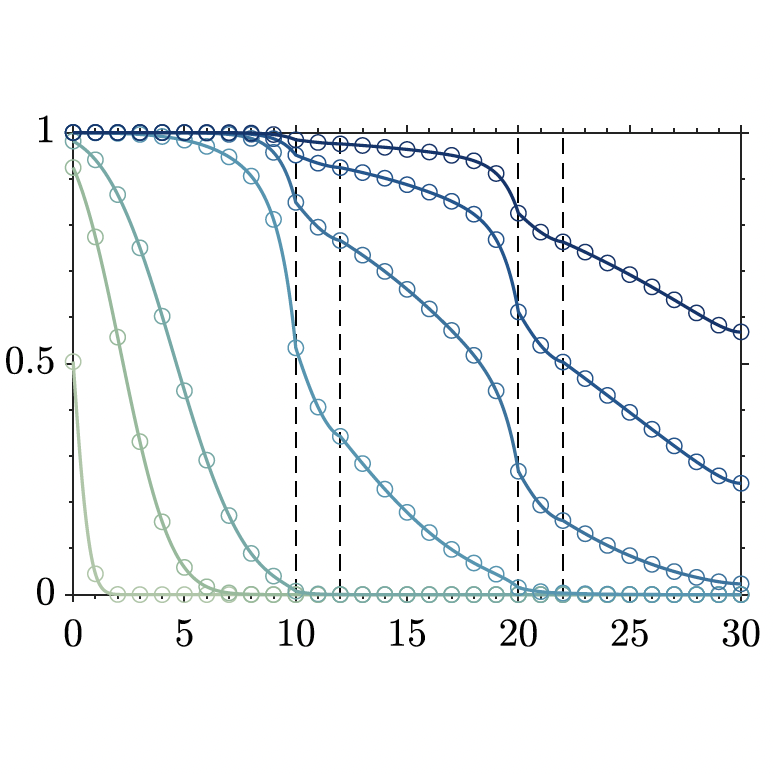
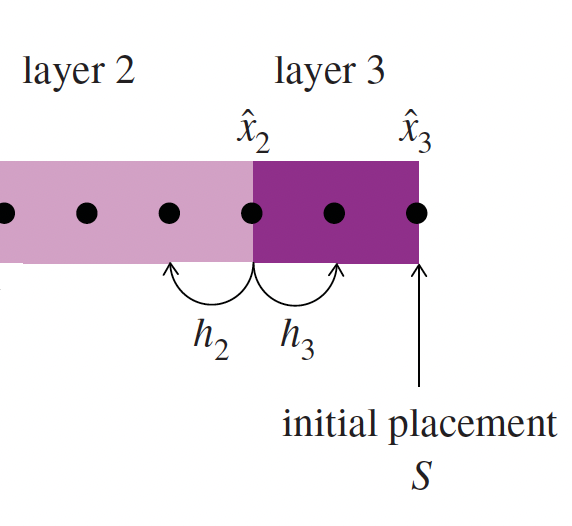
Multilayer advection diffusion reaction
Source: Carr (2020)

Drug delivery from multiple emulsions
Source: Pontrelli et al. (2020)
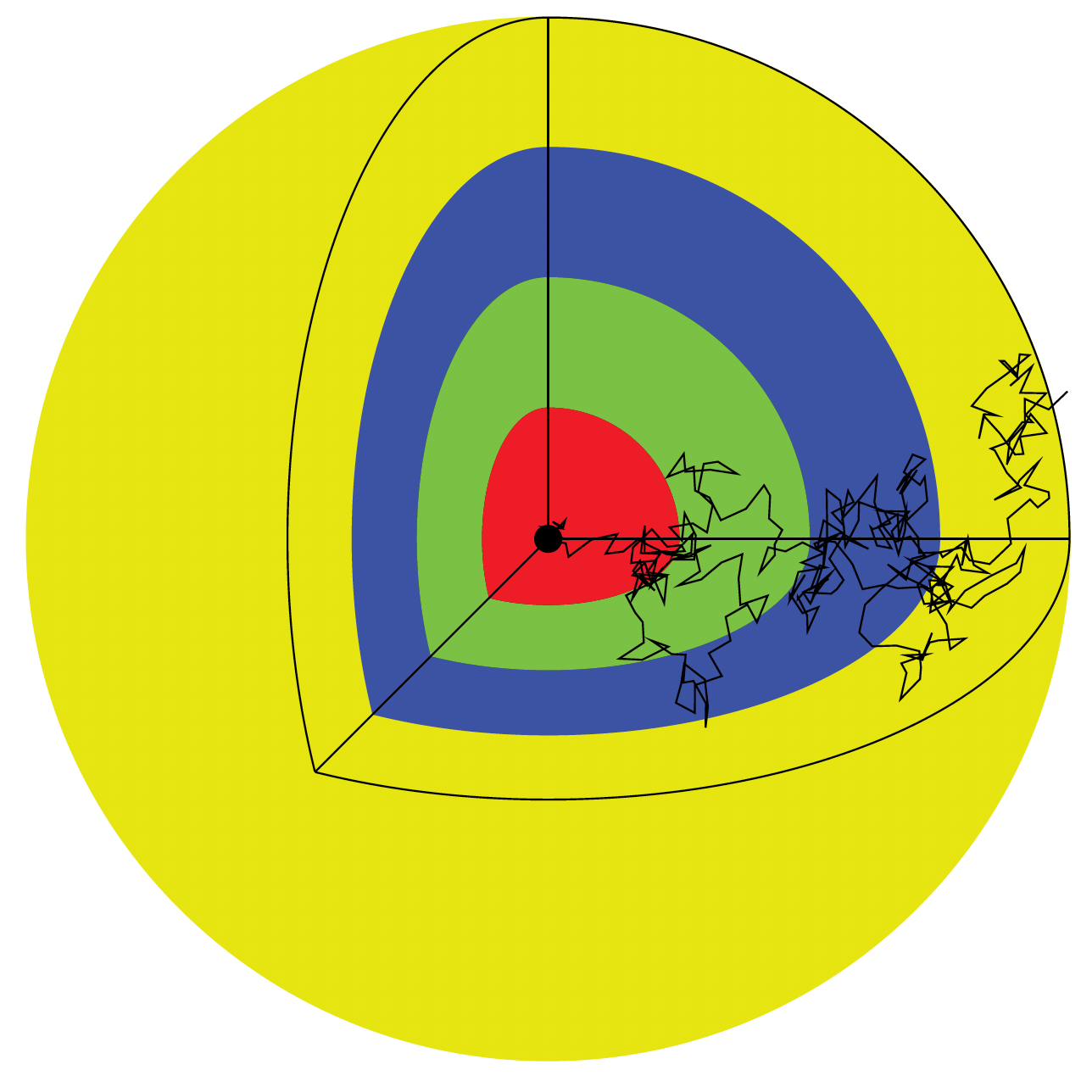
Mean exit time in heterogeneous spheres
Source: Carr et al. (2020)

Thermal diffusivity of layered materials
Source: Carr and Wood (2019)
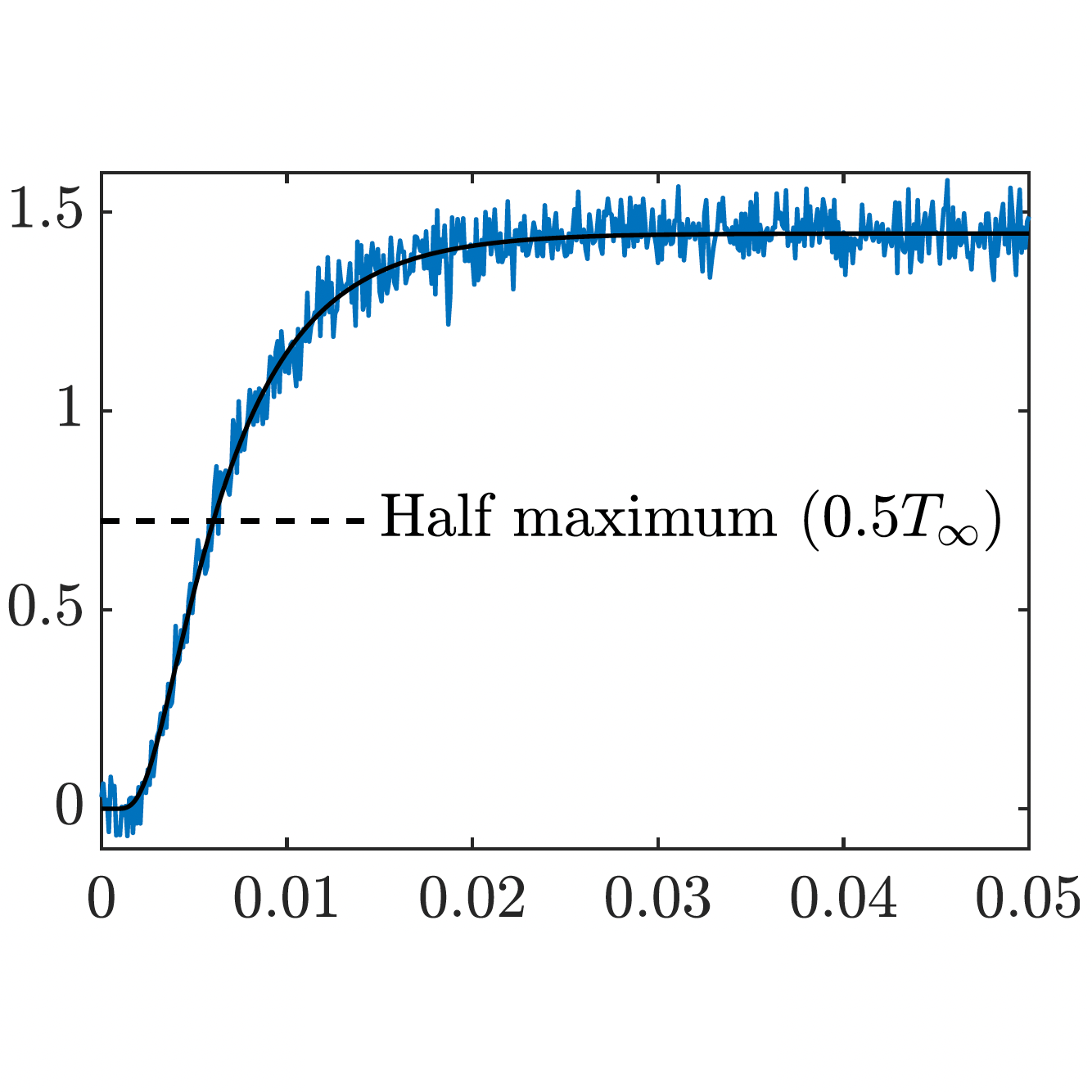
Thermal diffusivity of solid materials
Source: Carr (2019)
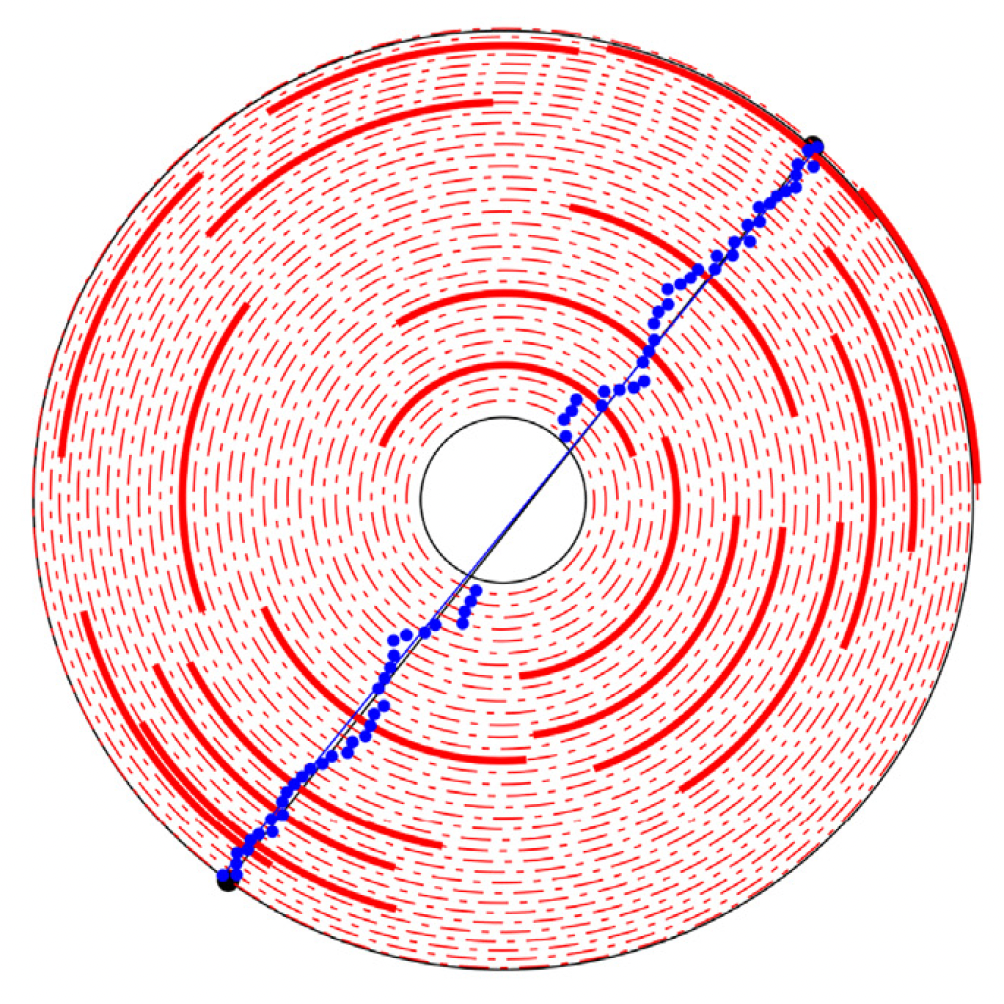
Virtual reconstruction of peeled timber
Source: Psaltis et al. (2018)
Drug deliverying microcapsules
Source: Carr and Pontrelli (2018)
Maximum particle lifetime for diffusion
Source: Carr and Simpson (2018)
Response times for groundwater flow
Source: Carr and Simpson (2018)

Two-scale modelling of transport
Source: Carr et al. (2016)

Two-scale modelling of groundwater flow
Source: Carr and Turner (2014)
Dual-scale model for wood drying
Source: Carr et al. (2013)
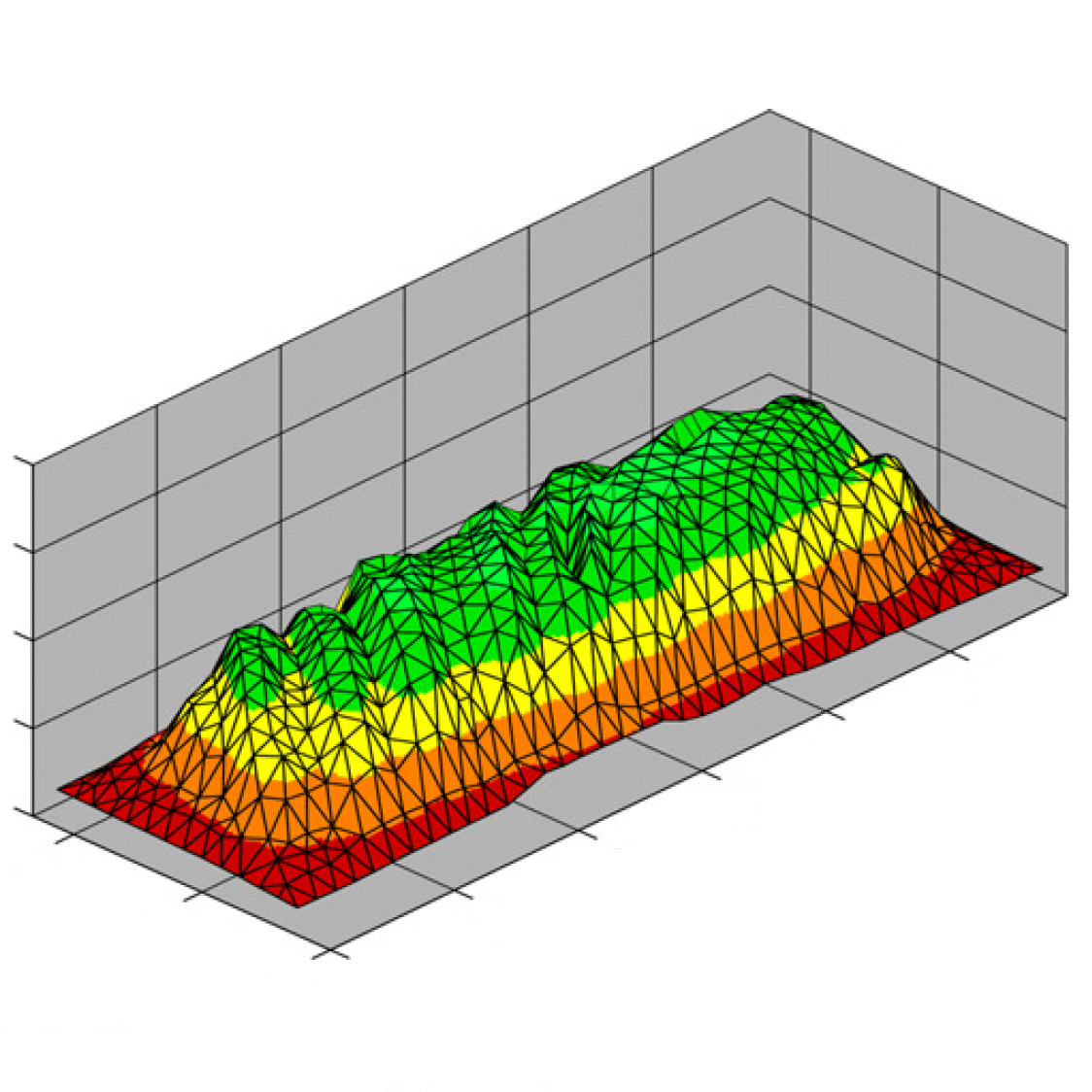
Simulating the drying process in wood
Source: Carr et al. (2013)

Simulating groundwater flow in soils
Source: Carr et al. (2011)
Supervision
Postdoctoral Fellows
- Riley Whebell (2024-). Supported by ARC Discovery Project Grant.
- Steven Psaltis (2015-2018). Supported by Forest and Wood Products Australia Research Grant. Publications: Psaltis et al. (2018), Kumar et al. (2021), Psaltis et al. (2021).
Doctor of Philosophy
- Luke Filippini (2024-) [Principal Supervisor].
- Dylan Oliver (2022-) [Principal Supervisor]. Publications: Oliver et al. (2024), Oliver et al. (2025).
- Hamish Murray (2020-) [Associate Supervisor]. Publications: Murray et al. (2022).
- Dr Nathan March (2017-2021) [Principal Supervisor]. Thesis: Analytical, numerical and macroscopic modelling approaches for heterogenous transport processes. Publications: March and Carr (2019), March et al. (2021a), March et al. (2021b).
- Dr Adam Redman (2015-2017) [Associate Supervisor]. Thesis: Modelling of vacuum drying of Australian hardwood species. Publications: Redman et al. (2017), Redman et al. (2018).
Master of Philosophy
- Obi Carwood (2024-) [Principal Supervisor].
- Luke Filippini (2022-2023) [Principal Supervisor]. Thesis: Surrogate models for diffusive transport in radially-symmetric media. Publications: Filippini et al. (2023).
- Jonah Klowss (2020-2021) [Associate Supervisor]. Thesis: Mathematical and computational models of tumour spheroids with cell cycle indicators. Publications: Klowss et al. (2022).
- Sean McInerney (2017-2018) [Associate Supervisor]. Thesis: Parameterising continuum models of heat transfer in heterogeneous living skin using experimental data. Publications: McInerney et al. (2019).
Honours
- Dylan Oliver (2021) [Sole Supervisor]. Thesis: New semi-analytical solutions for coupled multispecies advection-diffusion equations.
- Hamish Murray (2019) [Associate Supervisor]. Thesis: Optimisation of the Australian Football League Fixture.
- Nathan March (2016) [Sole Supervisor]. Thesis: Analytical and numerical solution methods for the one-dimensional multilayer diffusion problem. Publications: Carr and March (2018).
Summer/Undergraduate
- Obi Carwood (2023-2024) [Sole Supervisor].
- Luke Filippini (2021-2022) [Sole Supervisor]. 2021-2022 AMSI Vacation Research Scholarship. Publications: Carr and Filippini (2023).
- Obi Carwood (2021-2022) [Sole Supervisor].
- Joshua Wilson (2020-2021) [Co-Supervisor]. Publications: Carr et al. (2022b).
- Daniel VandenHeuvel (2020-2021) [Co-Supervisor]. Publications: Simpson et al. (2021), Carr et al. (2022b).
- Dylan Oliver (2020-2021) [Sole Supervisor]. Publications: Carr et al. (2022a).
- Jonah Klowss (2019-2020) [Sole Supervisor]. 2019-2020 AMSI Vacation Research Scholarship. Publications: Carr and Klowss (2020).
- Joshua Wilson (2019-2020) [Co-Supervisor]. 2019-2020 AMSI Vacation Research Scholarship.
- Christyn Wood (2018-2019) [Sole Supervisor]. 2018-2019 AMSI Vacation Research Scholarship. Publications: Carr and Wood (2019).
- Ryan Watson (2018-2019) [Sole Supervisor]. 2018-2019 AMSI Vacation Research Scholarship.
- Kaitlyn Brown (2018-2019) [Co-Supervisor].
- Jesse Huppert (2018-2019) [Co-Supervisor].
- Sean McInerney (2016-2017) [Co-Supervisor]. 2016-2017 AMSI Vacation Research Scholarship. Publications: Simpson et al. (2017).
Potential Projects
I have several projects available for summer vacation, Honours, Masters and PhD students. Please email me (elliot.carr@qut.edu.au) for further information.
Funding
Australian Research Council Discovery Project (2023-2025)
Ian Turner, Marie-Luise Wille, Elliot Carr, Ian O'Hara. Transforming Australian bio-based industries through multiscale modelling ($478K)
Australian Research Council Discovery Early Career Researcher Award (2015-2018)
Elliot Carr. Two-scale numerical modelling of coupled transport in heterogeneous media ($312K)
Forest and Wood Products Australia Research and Development Funding Program (2015-2018)
David Lee, Ian Turner, Troy Farrell, Elliot Carr. Improving returns from southern pine plantations through innovative resource characterisation ($1.2M)
Education
Doctor of Philosophy (2009-2012)
Queensland University of Technology. Study Area: Applied and Computational Mathematics. Thesis: Exponential integrators and a dual-scale model for wood drying.
Honours: Vice-Chancellor's Top-Up Scholarship, Outstanding Doctoral Thesis Award (top 5% of graduates university-wide).
Bachelor of Applied Science (Honours) - Mathematics (2008)
Queensland University of Technology. Study Area: Applied and Computational Mathematics, Statistics. Thesis: Exponential integrators and their application to solving Richards’ Equation.
Honours: University Medal (top 0.5% of graduates university-wide), Dean’s Award – Bachelor of Applied Science (Honours) (Mathematics) (top graduate), GPA 7.0/7.0.
Bachelor of Mathematics (2005-2007)
Queensland University of Technology. Study Area: Applied and Computational Mathematics, Statistics.
Honours: Vice-Chancellor's Scholarship, Dean’s Award – Bachelor of Mathematics (top graduate), GPA 7.0/7.0.
Teaching
MXB326 Computational Methods 2 (2021-present)
Third year course covering transport equations, finite volume methods, Newton methods for nonlinear systems, Krylov subspace methods for linear systems, MATLAB programming.
MXB103 Introductory Computational Mathematics (2017-present)
First year course covering time stepping schemes for ODEs, interpolation, numerical methods for solving nonlinear equations, numerical differentiation and integration, LU and Cholesky factorisations, MATLAB programming.
MZB127 Engineering Mathematics and Statistics (2024-present)
First year course covering multivariable functions, multivariable differentiation, multiple integrals, first and second order differential equations, systems of first order differential equations, eigenvalues and eigenvectors, MATLAB programming.
MXN400 Mathematical Research Training (2019-present)
Honours year course covering formulating a research problem, literature searching, citations and reference management tools, mathematical typesetting using LaTeX, writing for the mathematical sciences, presenting for the mathematical sciences.
EGB242 Signal Analysis (2018-2021)
Second year course covering Fourier series, complex Fourier series, Fourier transform, discrete Fourier transforms, Laplace transform, Z transform, MATLAB programming. Taught maths component only.
AMSI Winter School (2019)
Graduate Course (Computational homogenization of complex heterogeneous media) covering diffusion in heterogeneous media, homogenization techniques, finite volume methods on unstructured meshes, MATLAB programming.
MXB222 Computational Linear Algebra (2015)
Second year course covering direct methods for linear systems, storage of and direct methods for banded and sparse linear systems, vector and matrix norms, iterative methods for linear systems and eigenvalue problems, MATLAB programming.
MAB127 Mathematics for Engineering 2 / MAB122 Linear Algebra and Multivariable Calculus (2011-2012)
First year course covering partial derivatives, multiple integrals, equations of lines, planes and curves, vectors and matrix operations, Gaussian elimination, determinants and inverses, dot and cross products, orthogonality, eigenvalues and eigenvectors.
MAB100 Mathematical Sciences 1A (2009)
First year course covering functions, single-variable calculus, vectors and matrices, systems of linear equations, complex numbers.
Tutoring (2007-2012)
As a student, I tutored many courses at QUT including MAB312 Linear Algebra, MAB420 Computational Mathematics 2, MAB112 Mathematical Sciences 1C and MAB141 Mathematics and Statistics for Medical Science.
Talks
Invited
- Random walks with absorbing boundaries
(2023) Australian and New Zealand Industrial and Applied Mathematics (ANZIAM) Conference, Cairns, Australia, 5-9 February.
- Analytical insight into random walks on finite domains with absorbing boundaries
(2022) School of Mathematical Sciences Colloquium, University of Adelaide, Australia, 30 September.
- Cancelled due to COVID-19
(2020) Numerical methods for complex high-dimensional systems, Sydney, Australia, 13-14 July.
- Semi-analytical solutions for transport PDEs in heterogeneous media
(2020) Monash Workshop on Numerical Differential Equations and Applications, Melbourne, Australia, 10-14 February.
- Coarse-scale simulation of heterogeneous flows: application to groundwater modelling
(2019) Forum “Math-for-Industry” (FMFI), Auckland, New Zealand, 18-21 November.
- Multiscale Modelling of Groundwater Flow
(2016) Forum “Math-for-Industry” (FMFI), Brisbane, Australia, 21-23 November.
Contributed
- Perturbation solution for heat/mass transfer across an irregular interface
(2022) Australian and New Zealand Industrial and Applied Mathematics (ANZIAM) Conference, Virtual, 6-11 February.
- New semi-analytical solutions for advection-diffusion-reaction equations in layered media
(2021) Australian and New Zealand Industrial and Applied Mathematics (ANZIAM) Conference, Virtual, 31 January-5 February.
- Novel calculation of thermal diffusivity from laser flash experiments
(2020) Australian and New Zealand Industrial and Applied Mathematics (ANZIAM) Conference, Hunter Valley, Australia, 2-6 February.
- Computational simulation of complex fine-scale heterogeneous flows using homogenization and coarse-graining approaches
(2019) International Congress on Industrial and Applied Mathematics (ICIAM), Valencia, Spain, 15-19 July.
- Drug delivery from multi-layer micro-capsules: how can we estimate the release time?
(2019) International Conference on the Mechanical Behaviour of Materials (ICM), Melbourne, Australia, 11-14 June.
- Calculating thermal diffusivity from laser flash experiments
(2019) Australian and New Zealand Industrial and Applied Mathematics (ANZIAM) Conference, Nelson, New Zealand, 3-7 February.
- Novel calculation of response times for groundwater flow
(2018) Computational Techniques and Application Conference (CTAC), Newcastle, Australia, 27-30 November.
- Calculating how long it takes for diffusion processes to reach steady state: application to groundwater flow
(2018) Australian and New Zealand Industrial and Applied Mathematics (ANZIAM) Conference, Hobart, Australia, 4-8 February.
- Using volume averaging to correct the boundary conditions in macroscale models of multilayer diffusion
(2017) Australian and New Zealand Industrial and Applied Mathematics (ANZIAM) Conference, Hahndorf, South Australia, 5-9 February.
- Multiscale computational modelling of gradient-driven transport in heterogeneous media
(2016) Computational Techniques and Applications Conference (CTAC), Monash University, Melbourne, Australia, 27-30 November.
- Semi-analytic solution of the one-dimensional multilayer diffusion problem with an application to macroscopic modelling
(2016) Australian and New Zealand Industrial and Applied Mathematics (ANZIAM) Conference, Canberra, Australia, 7-11 February.
- Two-scale PDE-based numerical modelling of gradient-driven transport in heterogeneous materials
(2015) Engineering Mathematics and Applications Conference (EMAC), Adelaide, Australia, 6-9 December.
- Semi-analytic solution of the one-dimensional multilayer diffusion problem with an application to macroscopic modelling
(2015) Queensland Branch of ANZIAM (QANZIAM) Annual Meeting, University of Queensland, Brisbane, Australia, 25 November.
- Two-scale numerical modelling of flow in porous media with fine-scale heterogeneity
(2015) Maths Seminar Series, Queensland University of Technology, Brisbane, Australia, 5 June.
- Two-scale computational modelling of unsaturated water flow in soils exhibiting small-scale heterogeneity
(2015) Australian and New Zealand Industrial and Applied Mathematics (ANZIAM) Conference, Gold Coast, Australia, 1-5 February.
- Exponential integrators and two-scale approaches for unsaturated water flow in heterogeneous soils
(2014) Novel Reservoir Modelling and Simulation Group (NORMS) Meeting, Imperial College London, 26 November.
- Two-scale computational modelling of unsaturated flow in soils exhibiting small scale heterogeneity
(2013) Mathematics of Planet Earth (MPE) Conference, Melbourne, Australia, 8-12 July.
- Comparative performance of stiff ODE solvers for simulating transport in heterogeneous porous media
(2012) Computational Techniques and Applications Conference (CTAC), Queensland University of Technology, Brisbane, Australia, 23-26 September.
- Some results relating to Krylov subspace approximation of the matrix function $\varphi(A)b = A^{−1}(e^{A} − I)b$
(2010) Computational Techniques and Applications Conference (CTAC), University of New South Wales, Sydney, Australia, 28 November-1 December.
- A mass conservative mesoscopic drying model
(2010) International Drying Symposium (IDS), Magdeburg, Germany, 3-6 October.
- Efficient simulation of unsaturated flow in heterogeneous soils using an exponential integrator
(2009) Queensland Branch of ANZIAM (QANZIAM) Annual Meeting, Boonah, Queensland, 24-25 October.